Diving into Halton Sampling in Your Renderer

When you swap out rand() for a low-discrepancy sequence like Halton, you expect smoother, faster-converging Monte Carlo renders. But Halton isn’t just “fancier randomness”—it has its own quirks that can trip you up when you mix 1D and 2D draws.

1. The Halton “Spreadsheet” Analogy

Imagine your pixel sampler has an infinite spreadsheet of precomputed values:

• Rows ≙ which pixel-sample you’re on
• Columns ≙ which dimension (lens jitter, Fresnel coin-flip, microfacet lobe) you’re reading

Crucially, each column by itself—if you walk down the rows—forms a uniform Halton stream. But reading across one row (all the dims of a single sample) is just one point’s coordinates, not a uniform 1D series.

2. The Interference Bug in the Old Sampler

My initial implementation is something like this.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

uint sampleIndex = 0;

void reset() { sampleIndex = 0; }

float get1D() {
  // bump row, then read column 0
  return radicalInverse(base2, ++sampleIndex);
}

vec2 get2D() {
  // bump row *again*, then read cols 0&1 of that new row
  uint32_t s = ++sampleIndex;
  return { radicalInverse(base2, s),
           radicalInverse(base3, s) };
}

And then for each ray sample, I use them as the sampled uniform number to feed the Sample_f function.

1
2
3
4
5

float uc     = sampler.get1D(); // row → 1, reads col 0  
vec2 u    = sampler.get2D(); // row → 2, reads cols 0&1  

Sample_f(Vector3f wo, Float uc, Point2f u,
        TransportMode mode, BxDFReflTransFlags sampleFlags)

Note that I never called reset once. So uc basically gives all the number on the even rows of the Halton table’s first column (i.e. Halton[1][0], Halton[3][0], Halton[5][0] …) across all the samples. And u gives something similar, all the odd rows of the table’s first and second column across all the samples. The distribution of uc across all the samples are actually (0.5, 0.75, 0.625...) and it never goes below 0.5 so it’s not a uniform distribution across all the samples. Similar applies to the distribution of u.

Weird rendering caused by non-uniform numbers.

The reason I didn’t find the bug is because initially, is because for each sample, I only called float uc = sampler.get1D();, and never called vec2 u = sampler.get2D(); So the sequence of uc I’m getting is exactly the first column of the Halton table, which is uniform across the samples.

Correct rendering using the updated Halton sampler

3. The “Correct” Halton Sampler API (from PBRT, simplified)

To fix it, we split “which row” from “which column”:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class HaltonSampler {
  uint32_t row       = 1;  // which pixel‐sample
  int      column    = 0;  // which dimension of that sample

public:
  // Call once at the start of each primary ray (each pixel‐sample)
  void startSample() {
    row++;
    column = 0;
  }

  // Pull one 1D sample (Fresnel, etc.)
  float get1D() {
    float v = radicalInverse(prime[column], row);
    column++;
    return v;
  }

  // Pull a 2D sample (microfacet, lens, etc.)
  vec2 get2D() {
    float x = radicalInverse(prime[column],   row);
    float y = radicalInverse(prime[column+1], row);
    column += 2;
    return { x, y };
  }
};

Now:

1. startSample() → move down one row (new pixel sample), reset to first column
2. get1D() or get2D() → read successive columns of that row

4. Why This “Just Works” in a Path Tracer

• Per-pixel: you do

  1 2 3 4 5

  sampler.startSample(); // row = i float coinFlip = sampler.get1D(); // reads column 0 of row i vec2 microU = sampler.get2D(); // reads cols 1&2 of row i float lensU = sampler.get1D(); // reads column 3 of row i // … further bounces pull more columns …

• Uniformity arises across pixel-samples:

  • Looking at all coinFlip values is column 0 down rows → the base-2 Halton sequence → nicely stratified
  • Looking at all microU.x is column 1 down rows → base-3 Halton → stratified in that dimension
  • And so on

Within a single path you just grab different dims of one quasi-random point; across the whole image each dimension covers [0,1] evenly.

5. Caveats

1. If You Never Call startSample()

• What happens

  • row stays at its initial value (e.g. 1).
  • column increments on each get1D()/get2D().
  • You always read row 1, columns 0,1,2,3,…

• Returned values

  1 2 3 4 5 6 7

  //pixel sample 1 u = get1D(): radicalInverse(prime[0], 1) v = get1D(): radicalInverse(prime[1],1) //pixel sample 2 u = get1D(): radicalInverse(prime[2], 1) v = get1D(): radicalInverse(prime[3],1)

• Impact

  Each parameter samples u across pixel, is a sequence on the initial row with a fixed stride.

  Let’s say for each pixel, you request one u = get1D(), then u across pixel samples is just a row from the table, which is not uniform.

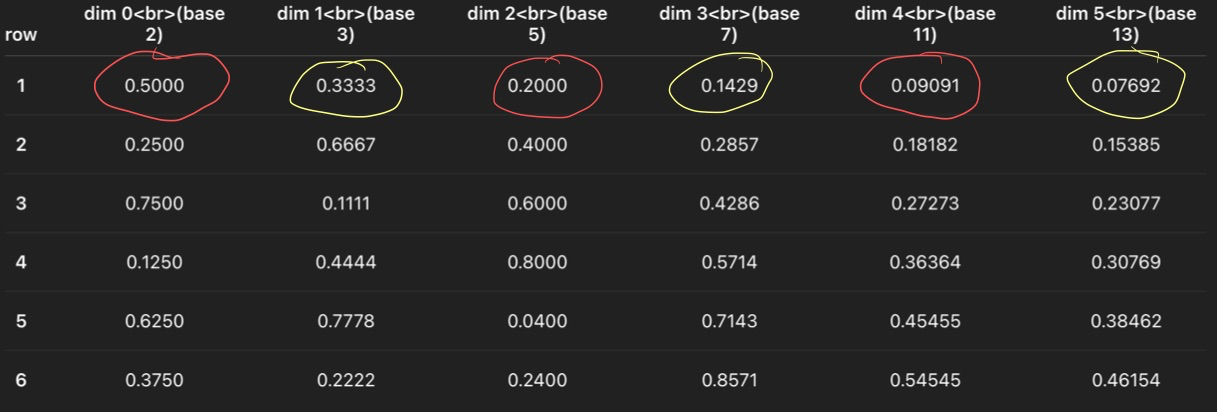
In above example, u are circles in red, v are circled in yellow. Both of them are not uniform.

2. If You Skip Resetting column in startSample()

1
2
3
4

void startSample() {
  row++;      
  // OOPS: column is NOT reset → carries over from last pixel
}

• What happens
  • row advances per pixel, but column keeps climbing across pixels.
  • Pixel 1 might read columns 0,1,2; Pixel 2 now reads columns 3,4,5; Pixel 3 reads 6,7,8; …
• Returned values
  • Pixel 1: u = get1D→col0, v = get2D→col1, …
  • Pixel 2: u = get1D→col2, v = get2D→col3, …
  • Pixel 3: u = get1D→col4, …
• Impact
  • Each individual call is still reading a single Halton column down the rows
  • But the mapping of “Fresnel”→col0, “microfacet”→cols1/2, “lens”→col3, etc. drifts unpredictably between pixels.
    • Larger primes push more weight near zero, so as you march down that diagonal your samples systematically shift. i.e. Not uniform.
  • Visually, each parameter samples, across all pixels, forms a diagonal walk on the table, which is not uniform.

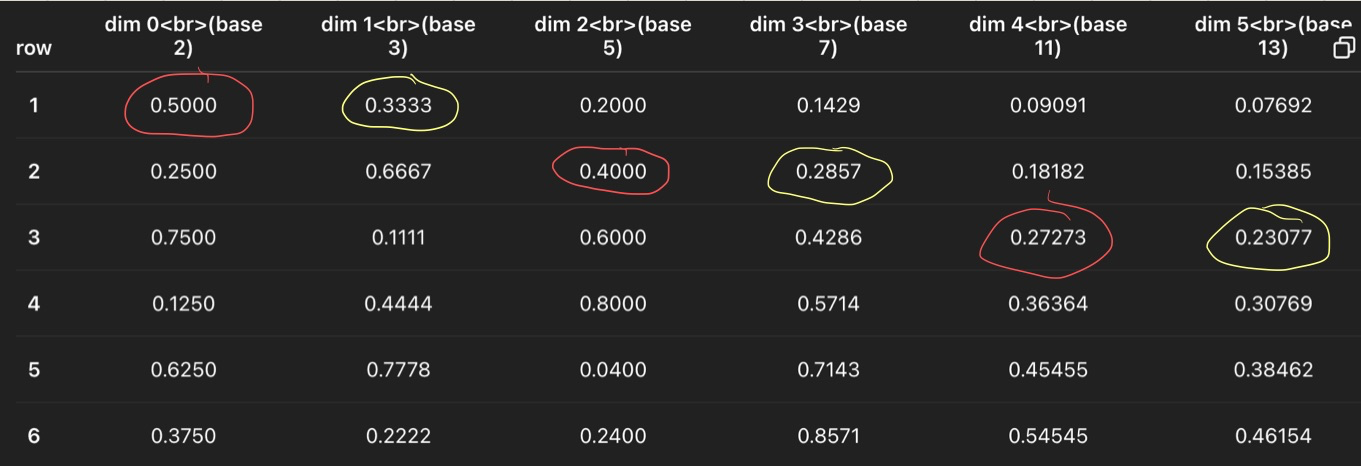
In above example, u are circles in red, v are circled in yellow. Both of them are not uniform. Though slightly better than previous one, since we move across rows.

3. If You Don’t Advance the Row in startSample()

1
2
3
4

void startSample() {
  // OOPS: no row++, so row stays fixed
  column = 0;
}

• What happens

  • row is always the same (say 0),
  • column resets each pixel and then increments as you call get1D()/get2D().

• Returned values per pixel

  1 2 3 4 5 6 7

  //pixel 1 get1D() → radicalInverse(prime[0], 1) get1D() → radicalInverse(prime[1], 1) //pixel 2 get1D() → radicalInverse(prime[0], 1) get1D() → radicalInverse(prime[1], 1)

• Impact

  • Each parameter samples, across all pixels is just reading the same value.
  • No variation, no uniformity over the image.

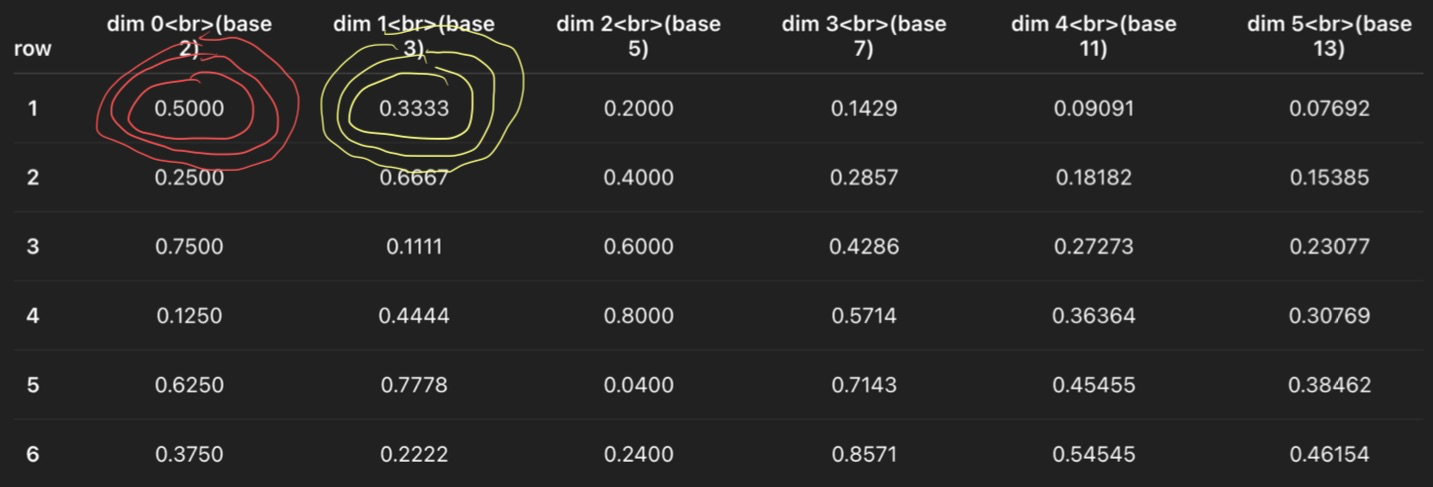
In above example, u are circles in red, v are circled in yellow. Both of them stays the same value across pixels.

Again, the correct version

1
2
3
4

void startSample() {
    row++;
    column = 0;
}

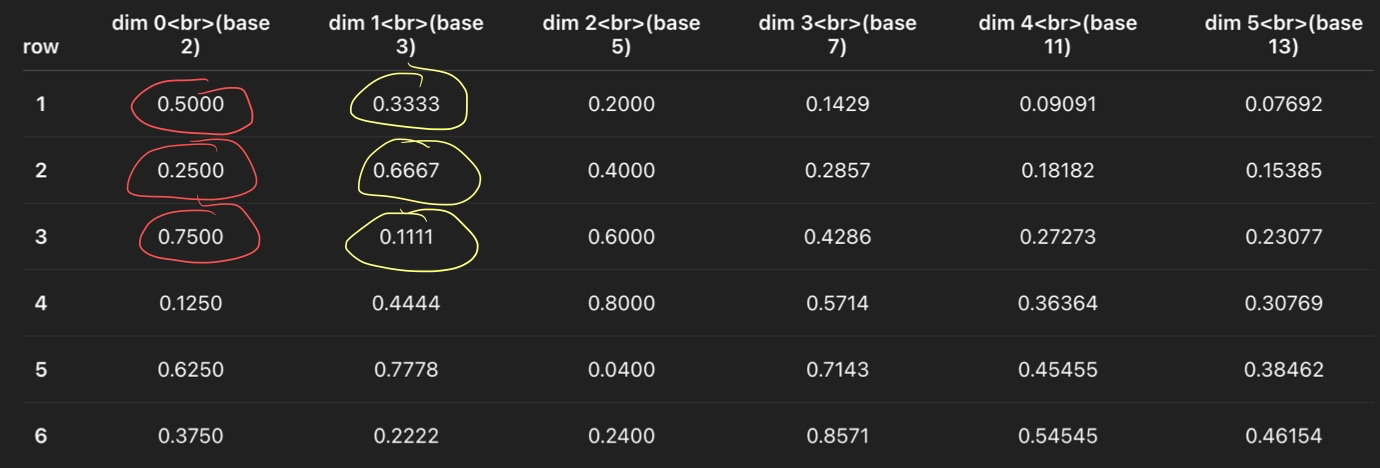
Now you can see both u and v are uniform across pixels.

6. TL;DR

• Don’t bump your low-discrepancy index in both get1D() and get2D(). That “phase-shifts” your samples. Making them not uniform across samples.
• Do maintain:
  • one counter per pixel (row) advanced once by startSample(),
  • one counter per random number (column) advanced by each get1D()/get2D().
• Result: perfect coordination between Fresnel flips, BSDF directions, lens jitter, shadow-ray uniforms—all with QMC convergence benefits.