Point Matching - Voting Tree

Point Matching - Voting Tree

January 17, 2022

Chapter 1: Introduction

Point Matching Problem:

Given two polygons (each is defined by set of points), return the best point matching between the polygons.

To give you a better idea of what a point matching may be look like, here’s an example:

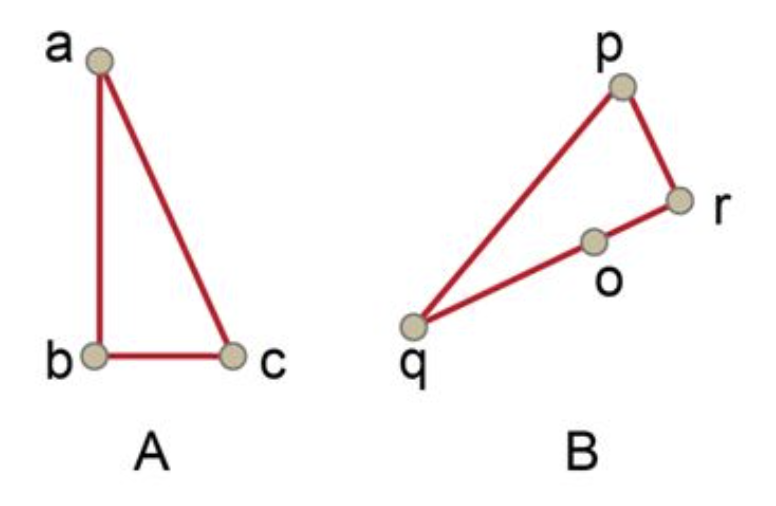
image-20211021214429442

You can tell that, the match (a,p), (b,r), (c,q) is not a good match, because $\angle A \ll \angle P$.

In this case, since $ \triangle ABC \sim \triangle QRP$, so we get a good match (c,p),(b,r),(a,q)

But you may ask, Is that match the best match? What is a best matching mathematically? What if there’s no mathematically similar polygons? Well, these problems can be solved by giving our definition of “Good Match”. Through this case, you may get a sense of what is a good match, that is, we can define the how well a match is by the similarity between matching points.

A mathematic description is given as below.

Good Matching:

Similarity Function:

Follow the principle that: Define how well a match is by the similarity between matching points. We have to firstly define a similarity function between two sets of points.

Referencing the similarity function from: Zhang Yuefeng. A fuzzy approach to digital image warping. IEEE Computer Graphics and Applications, 1996, 16(6):34~41

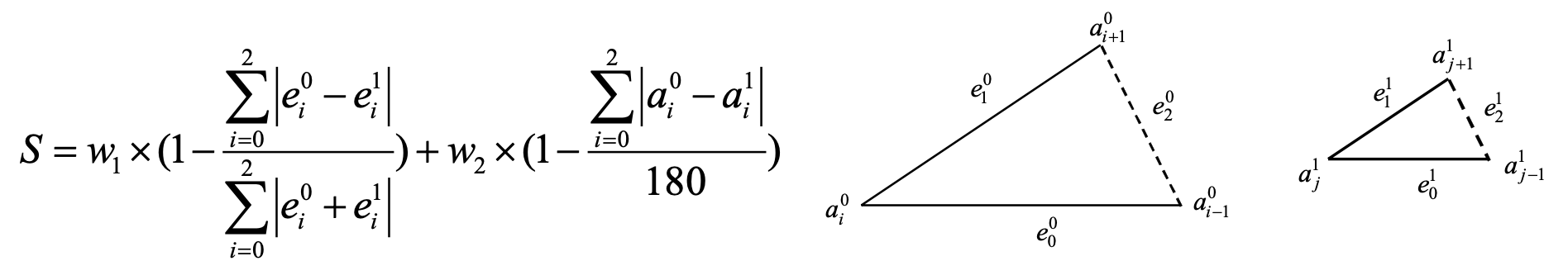
image-20211021221008037

Let’s take a look at the similarity function.

Suppose we have two triangles, edges and angles are denoted as above. The Similarity between these two triangles are defined as above. Note that the Similarity Function has two terms:

  • The Edge similarity term: measures the similarity with respect to length of edges
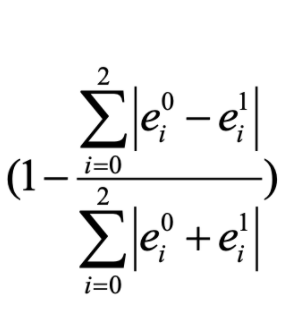
image-20211021225903082
  • The Angle similarity term: measures the similarity with respect to angle
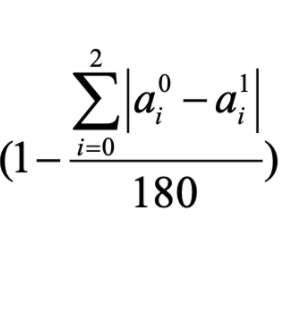
image-20211021230014758

The similarity value is the weighted sum of the two similarity term, by default, we set both weight to 0.5, i.e. $w_1 = 0.5,w_2 = 0.5$.

It’s pretty obvious that, the higher the value is, the higher the similarity is.

$Similarity(T_1,T_2) ==1 \iff T1\triangleq T2$

What is a best matching?

Now we know that, what means a good matching between two triangles.

$best_{match}(set(A),set(B)) = max(Similarity(set(X),set(Y)), where\ X.size== Y.size==3)$

Note that, the higher the similarity function value, the better the matching is. In this way, to find out the best triangle matching, we only have to find out two ordered sets of point pairs (with a size of 3), which have the highest similarity function value. And such pair is the best matching by our definition.

Actually, we can extend this Similarity Function to polygons with more than 3 edges.

Best matching, mathematically

$best_{match}(set(A),set(B)) = max(Similarity(set(X),set(Y))$

$where\ X.size== Y.size==min(A.size(),B.size())$

The Similarity of between 2 size n sets match is defined as below:

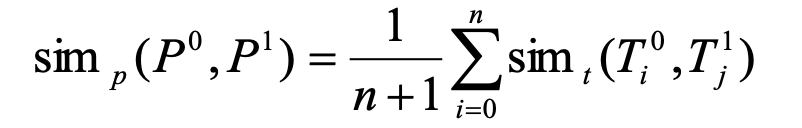
image-20211022000404251

Which is simply the average of all correspoding triangles’ similarity. (T means Triangle)

Match Representation: Tree

To find out the best possible match, we have to traverse all possible match sequence, but how do we represent an ordered match between two sets of points? The answer is tree.

We use a tree node, formed by a point pair to denote a possible match. So a possible node is (a,p), and there’s m*n (m = setA.size(), n = setB.size()) possible nodes in total. And the children of node (a,p) should be next possible match, in this case, if we only take clockwise move into account, the next possible match is either (c,r) or (c,o).

image-20211021214429442
You may ask, why not (c,q) be the next possible match? This is because we have to follow another rule.

Yet another important rule: Monotonous

The word monotonus, in this context, meaning moving in the same direction from begining to the end. This means that, you can’t go from r to q (clockwise), and then go from q to o (counter-clockwise). Think about it, a matching subsequence (c,r)(b,q)(a,o) breaks the rule of monotonicity. If you connect $RQ$ and $QO$, you will find that $RQ$ overlaps with $QO$.

In fact, you will find out that generally, if a set of points is not connected in a monotonous order (in the same direction), overlapping and crossing edge could happen.

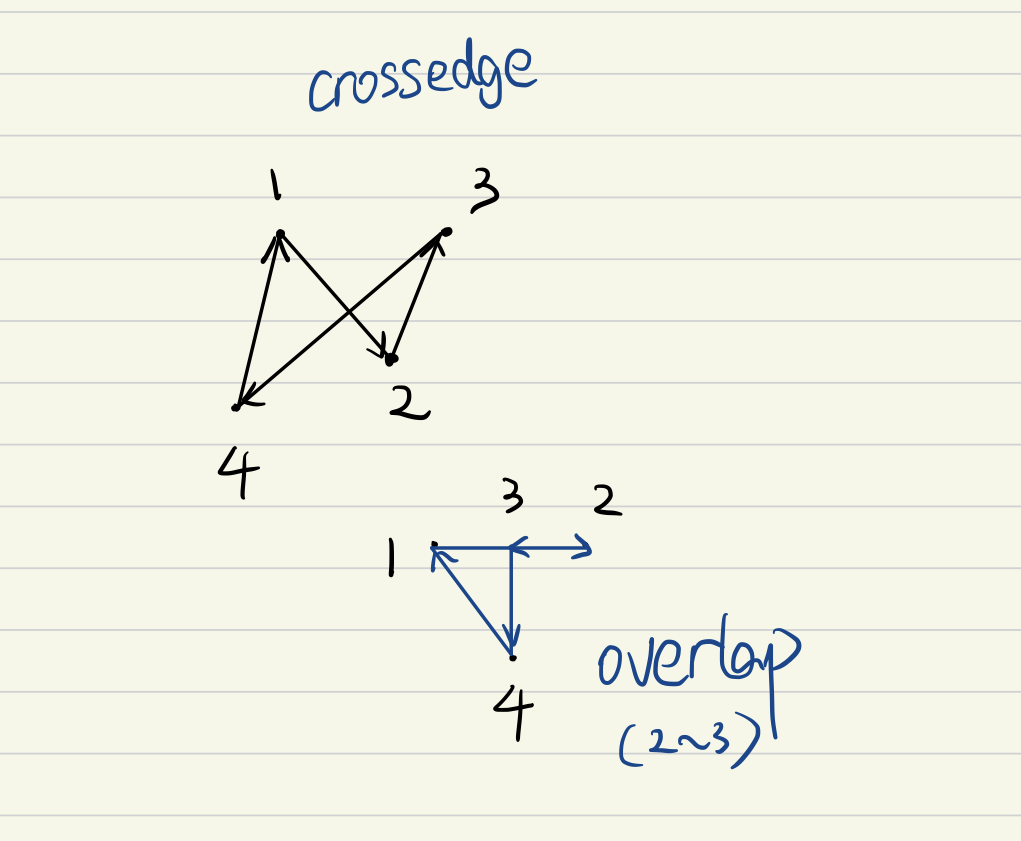
PNG图像

So inorder to conform to the monotonous rule, the point matching should be move in a certain and unchanged direction, either clock-wise or counter clockwise. For simplicity, we assume both of the polygons moves clockwise. ( This leaves a problem in the case of mirrored polygon matching, because in mirrored polygons, two polygons are connected in different direction )

Although we can simply don’t take mirrored polygons into account, an intuitive concept solution is given at the end of the report.

Since we only allow clockwise moves, (a,p)(c,q) is not a valid match sequence.

How many starting node?

On first thought, you may assume that there’s m*n (m = setA.size(), n = setB.size()) starting point. However, the nodes in the triangle are logically equivalent. In the example, setA has a fewer size of 3, which means in next possible match, the first polygon can only move one step clockwise. And you may already find that, once the starting point of polygon A is fixed, the possible match sequence of A is fixed. However, there’s 4 different possibilities of polygon B with a fixed starting point.

So in this case, we actually have max(m,n) staring nodes. And for simplicity, we assume that the polygon A always starts at point A.

Sample Case Tree:

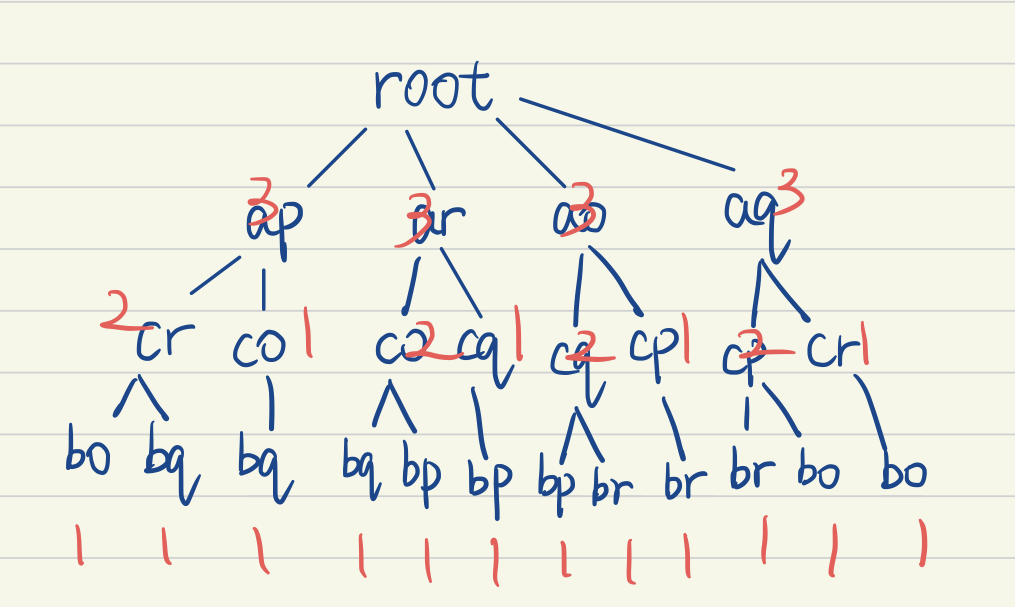
With all that being said, all possible match sequences in the sample case are show as tree below.

PNG图像 2

Now we may came up with different methods to find out the best matching, in this representation, the highest average (or cumulative) similarity path from root to leaf. But firstly let me simply introduce some other related works.

Input Specification:

Firstly give the number of indicies in each polygon, m and n. Then for next m+n line, each line is consist of x and y coordinate of the index (m first then n) . The points in each polygon are given in clockwise order, and indexed as 1、2、3…n.

Output Specification:

Return the best match in the form of (index1,index2) for m lines (suppose m<n)

Sample:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#still the same sample, where line 1-4 are m1~m3, line 5-8 are n1~n4.
#the output (1,2)(2,3)(3,4) means m1 matches n2, m2 matches n3, m3 matches n4
input:
3 4
0 4
3 0
0 0
8 4
8 1
4.25 6
8 6
output:
(1, 2)
(2, 3)
(3, 4)

In general, this is a 2D point set registration problem, is the process of finding a spatial transformation (e.g., scaling, rotation and translation) that aligns two point clouds.

Many different methods have been proposed to solve this problem, from Graph theory, machine learning, and each of them have a different cost function to achieve, in this case, the similarity function.

For other algorithms on this problem (Click for more):

  • Iterative Closet Point
  • RANSAC
  • Fuzzy Graph Matching

Build Environment & To Run:

See ./code/README.md
Recommend to open with Typora.

Brief Description On STL Used

  • std::vector
    • std::vector is a sequence container for dynamic size array.
    • Elements in vector can be accessed by [] operator, iterators, and offsets to pointers to elements.
    • The storage of vector is handled automatically, and usually extra memory is allocated for the growth of the vector.
    • Each time we insert a element to the vector, as long as the extra memory isn’t exhausted, we don’t need to reallocate memory (memory reallocation is expensive).
    • Time Complexity:
      • Random Access: $O(1)$
      • Insertion or Remove at the end:$O(1)$
      • Insertion or Remove at the front: $O(n)$
  • std::function
    • std::function is a general wrapper for function, it can store any copyconstructible callable object.
    • Can be used to store lambda expressions, member functions etc.
    • One usage is to pass function to function (Like function pointers).
      • It has no call overhead
      • It can capture context variables
  • std::pair
    • This is used to store 2 different objects in a single unit.
    • Can be replaced by struct, but std::pair offers a easier way to do so.
    • To assign value a and b to a pair<int,int>
      • Pair = make_pair(a,b);
  • std::map (Actually can be replaced by set or vector)

    • This structure is used to store a key->value pair

    • The implementation of Red-Black tree ensures a key-sorted traversal order.

    • It is implemented by Red-black tree

      • Search:$O(log(n))$
      • Insert:$O(log(n))$
      • Space Complexity:$(O(n))$

    • The basic properties of a red black tree

      • It’s a self-balanced binary search tree
      • Each node is either red or black
      • Root is black
      • external nodes are black
      • the children of a red node is black
      • Any path from external node to root, the number of black nodes along the path are the same.

      A sample red-black tree

      image-20211028155810975
  • std::chrono
    • This library is used for tracking time with different type of precision.
    • An massive extension to the time.h
    • system_clock offers a wall clock
    • high_resolution_clock offers a clock with shortest tick period.
    • duration to represent a interval of time.

Chapter 2: Algorithm Specification Description

Solution 1:

Voting Tree Idea:

PNG图像 2

Now we can introduce the idea of voting tree. Basically a voting tree is for each unique path from root to the leaf, if the node is present in the path, the point match presented by this node gets a vote. The higher votes a match get, the more likely this match could be true. For the tree above, $AP$ have 3 votes, $AR$ have 3 votes too, so does $AO$ …

Soon you will find that for this tree, each match have exactly 3 votes. We can’t get any information out of the tree. This is obvious becuase we haven’t use the point pair information stored at each node. We’re just doing arrangement and combinations now.

Why Pruning?

If we don’t prune the tree (cut off some branches), the voting process can’t give us any useful information. So we have to prune the tree in advance, based on our similarity function. My prune idea is simple, compute the similarity between two triangles, formed by node, node->parent, node->child. If the similarity is above a certain threshold, meaning this tree extension could be valid, else, this tree extension is invalid.

Prune: First Round

1
2
3
4
5
6
7
Traverse from root to leaf
    for each node(node.depth>=2)
		for each node.child
		//means not similar enough
    		if(similar(node.parent,node,node.children)<threshold)
    			invalidate(node.children)
    			go deeper

First round pruning under a high threshold, we only invalidate those nodes(depth>=2)’ children.

In the best case, all nodes(depth>=3) except the best matching has been invalidated.

PNG图像 3

Note that this is actually a greedy algorithm pruning, for each time we only consider the local similarity. And we only leave those branches with high similarity.

Prune: Second Round

1
2
3
Traverse from depth 2 leaves to root:
	if(node has no valid children)
		invalidate(node)

This is intuitive since if a node(non-leaf) doesn’t have valid children, meaning the match itself is also invalid. In best case, there is only one valid path from root to leaf.

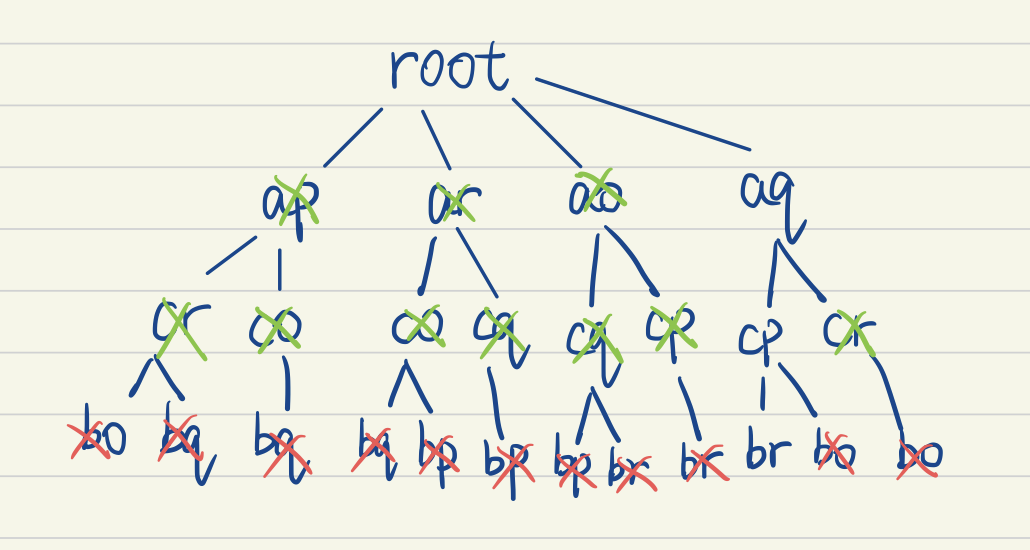
PNG图像 4

After the pruning, it’s obvious that, the path present yields a higher chance of best matching, so the tree can be used to vote. However, this algorithm relies heavily on the threshold, if the threshold is set low, it could produce wrong result, if set overly high, there could be no possible match. (Test on Part 3)

Trivia:

We have 2 similar but slightly different ways to determine the best match after voting to get the 2 bonus points.

How to Vote?

The vote process is a little bit tricky, different nodes have different vote counts. Some of the nodes may appear many times in different unique paths, but many nodes (mostly leaf nodes) only appear once in unique path. If we implement the idea of “unique path”, we have to visit some node many times, this requires backtracking technique. If we calculate the vote counts of node in advance, we only need to visit each node once, and that is simple to achieve by level order traversal.

Leaf node has exactly one vote count, and a non-leaf node.voteCount = sum(children.voteCount)

We have to compute from leaf to root.

PNG图像 6

After computing vote counts, we just traverse the tree, and vote for the matching, we keep a voting table. Table[node]+=node.voteCount

A Voting Table corresponding to the unpruned tree above.

PNG图像 7

How to decide the match out of Voting Table?

(Bonus is to have 2 different method determine the match)

Simple Idea: Get the first m-most votes

To use this method, #define _VOTE_ORDER

Suppose we have a voting table like this, we have to decide the best match out of the table, we just order them by votes. The result would be (a,q)(c,o)(c,r).

PNG图像 5

c appears twice in a matching sequence, so this simple idea is sometimes problematic for collision(c,o)and (c,r), although this isn’t very likely to happen with a properly set threshold.

An Improved Idea for anti-collision: Vote By Row

To use this method, #define _ROW_ORDER

Instead of finding the global max votes, we find out most vote in each row, and in order to avoid collision on a column, after finding the most vote in the row, we set all votes in that column to 0.

PNG图像 8

Implementation:

Tree Design:

Now we have to design our tree for implementation. Let’s think about what we need to keep in our tree.

  • PointPairs (Storing 2 points’ coordinates)

  • Indices (2 points’ indices in their polygon)

  • Depth (In pruning, we have to check whether if a node is of depth 2 or deeper )

  • Count (Storing the vote count)

  • isValid (Check if this node need to be pruned or not, check if it is a valid match)

  • Children (Storing all of it’s children’s address)

  • Parent (When doing similarity function, we have to pass 3 adjacent nodes, it comes handy if we just pass node, node->parent, node->children)

  • Credit (How many possibilities this node can move, further explanation below)

    Credit indicates how many possibilities a node can move, if a node’s children moves one step, it cost no credit, if more than one step, it cost n-1 credits. The number of credits also indicates the number of children a node can have.

    If a node has no credit, it can only move one step further thus have one child. Otherwise, it can move 1n+1 steps, costing 0n credits, thus having n+1 children.

    An illustration is below to show the idea of credit.

    PNG图像 9

With credit, you can easily figure out how many children each node can have.

TreeNode:

This is all information tree node CR, contains (before pruning).

PNG图像 10

Build Tree with pruning

Now we know that what a tree node is, we have to build the tree.

To get cut down time complexity, we can do pruning while building the tree.

Assume m<n, if not, swap them.

  1. Firstly, we build the depth 1 nodes (initial match), given with n-m credits each.

  2. For each depth 1 nodes we recursively build subtree by using helper function.

  3. In the helper function, we pass in a node

    1. if the node reaches depth m, means a full match, return
    2. if the node has no credit, means it can only move 1 step further, move, check similarity, if valid then extend and return, if not, don’t extend and return.
    3. if the node has some credits, means it can have credits+1 children, for each children, check similarity, if valid, extend, and pass children to the helper function for recursive call. if not valid, don’t extend, check the next children.

Futher Pruning (Second Round)

A top-down approach.

  1. Pass the node, if it has a valid children, it is valid. If not, set node.isValid to false, return.
  2. For each children of the node, if it has a valid children, it’s valid. If it doesn’t have children and is depth<m , meaning its children have been pruned while build tree, set node.isValid to false, return.
  3. Recursively call this function step 1~2

Level Order Traversal

To compute vote count bottom up, it would be convenient if we do level order traversal first.

We implement level order by 2 vectors, curr and next, indicating the nodes to process in this level and next level. We store the result in res vector. (vector<vector<TreeNode*>>)

  1. Push root node into curr
  2. While(curr is not empty), push curr to res, traverse all nodes in curr, for each node, we push all its children to next, finally swap(curr,next).

Compute Vote Count

  1. get level order traversal result
  2. start from the last level if it’s valid it has 1 vote count.
  3. For each level, it’s vote count equals to sum of its valid children’s vote count. Iteration ends at depth 1 (Don’t consider root)

Voting:

  1. traverse the tree by level order
  2. The corresponding term +=voteCount
    1. RowOrder: For each row in the table, find the max, set column of max to zero
    2. SimpleIdea: Find the m-most votes in the table.

Solution 2: Non-Voting

Because we apply greedy pruning to our tree, sometimes we may only get the local best match instead of global best. Remeber that, in chapter 1, our goal is to find a path from root to leaf, with a largest average similarity of corresponding triangles.

In this method, we simply don’t prune, and while we building tree, we keep track of the cumulative similarities of corresponding triangles. And we get the global best by simply find out the leaf node which havethe largest cumulative similarity.

This method is not reliant on parameters, and ensures a global best match under our definition.

TreeNode: add a cumulativeSim member

BuildTree: Almost the same, without pruning, keep track of cumulative similarity

Further Pruning: No need

Level Order Traversal: Same

Get Result:

  1. For the last level of the level order traversal (which is actually all the leaf nodes):
  2. Get the node with max cumulative similarity
  3. Trace back this node until root.

Chapter 3: Testing Results

Correctness Validation: With A Strict Threshold = 0.9

Case 1: Sample Case

1
2
3
4
5
6
7
pointsA.push_back(Point(0, 4));
pointsA.push_back(Point(3, 0));
pointsA.push_back(Point(0, 0));
pointsB.push_back(Point(8, 4));
pointsB.push_back(Point(8, 1));
pointsB.push_back(Point(4.25, 6));
pointsB.push_back(Point(8, 6));

ROW_ORDER: Correct

image-20211023011656249

SIMPLE_IDEA: Correct

image-20211023011856088

NON_VOTING: Correct

image-20211023011927482

Case 2: A 1x1 square and a 2x2 square

1
2
3
4
5
6
7
8
9
10
11
12
13
pointsA.push_back(Point(0, 0));
pointsA.push_back(Point(0, 1));
pointsA.push_back(Point(1, 1));
pointsA.push_back(Point(1, 0));

pointsB.push_back(Point(0, 0));
pointsB.push_back(Point(0, 1));
pointsB.push_back(Point(0, 2));
pointsB.push_back(Point(1, 2));
pointsB.push_back(Point(2, 2));
pointsB.push_back(Point(2, 1));
pointsB.push_back(Point(2, 0));
pointsB.push_back(Point(1, 0));

ROW_ORDER: Correct

image-20211023012132695

SIMPLE_IDEA: Wrong

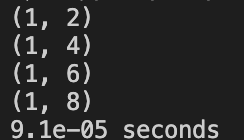
image-20211023012203375

NON_VOTING: Correct

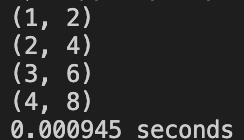
image-20211023012224618

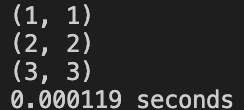
Case 3:A small triangle and a pentagon, the triangle is a subset of pentagon

1
2
3
4
5
6
7
8
9
pointsA.push_back(Point(0, 0));
pointsA.push_back(Point(0, 1));
pointsA.push_back(Point(1, 1));

pointsB.push_back(Point(0, 0));
pointsB.push_back(Point(0, 1));
pointsB.push_back(Point(1, 1));
pointsB.push_back(Point(2, 1));
pointsB.push_back(Point(2, 4));

ROW_ORDER: Correct

image-20211023012422694

SIMPLE_IDEA: Correct

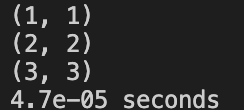
image-20211023012443966

NON_VOTING: Correct

image-20211023012508740

Case 4: Large Number(M=21,N=28), performance test

ROW_ORDER: 0.005 sec

SIMPLE_IDEA: 0.005 sec

NON_VOTING: 7.81 sec

Case 5: Mirror case

Test if the algorithm can get the best match if two polygons are mirrored to each other.

1
2
3
4
5
6
7
pointsA.push_back(Point(0, 4));
pointsA.push_back(Point(3, 0));
pointsA.push_back(Point(0, 0));
pointsB.push_back(Point(0, 0));
pointsB.push_back(Point(-3, 0));
pointsB.push_back(Point(0, 4));
pointsB.push_back(Point(8, 6));

ROW_ORDER: Not Found

image-20211023013827652

SIMPLE_IDEA: Not Found

image-20211023013829051

NON_VOTING: Wrong

image-20211023013749859

A solution will be proposed in chapter 4.

Correctness Table (For 5 test cases)

SIMPLE_IDEA ROW_ORDER NON_VOTING
YES YES YES
NO YES YES
YES YES YES
NOT APPLICABLE NOT APPLICABLE NOT APPLICABLE
NO NO NO

Hacking Cases During Peer Review

1
2
3
4 11
A:(-4,2)(-2,2)(-2,4)(-4,4)
B:(-2 -2)(-1 -2)(-1 -1)(2 2)(4 1)(5 3)(3 4)(3 6)(1 6)(1 4)(-2 -1)
SIMPLE_IDEA ROW_ORDER NON_VOTING
NO NO YES 
1
2
3
5 9
(2 -4) (4 -4)(6 -2)(4 0)(2 0)
(-5 5)(-8 2)(-8 -1)(-6 -1)(-6 -4)(-4 -4)(-4 -1)(-2 -1)(-2 2)
SIMPLE_IDEA ROW_ORDER NON_VOTING
NO NO YES

Major Problem:

  • The NON_VOTING Method has a comparatively high correctness rate, but the problem is that, it has a high time complexity, which makes it very hard to handle large cases（Acceptable M,N<25）.
  • The other 2 solutions has a somewhat simple and fast performance, but not that good in the correctness.

Parameters Test:

Only run sample cases, set threshold differently.

  • Threshold: 0.1
    • ROW_ORDER: Wrong
    • SIMPLE IDEA: Wrong
    • NON_VOTING: Correct
  • Threshold: 0.3
    • ROW_ORDER: Wrong
    • SIMPLE IDEA: Wrong
    • NON_VOTING: Correct
  • Threshold: 0.5
    • ROW_ORDER: Wrong
    • SIMPLE IDEA: Wrong
    • NON_VOTING: Correct
  • Threshold: 0.75
    • ROW_ORDER: Correct
    • SIMPLE IDEA: Wrong
    • NON_VOTING: Correct
  • Threshold: 0.9
    • ROW_ORDER: Correct
    • SIMPLE IDEA: Correct
    • NON_VOTING: Correct

A good general threshold would be around 0.8~0.9.

Correctness Table: For 5 thresholds

SIMPLE_IDEA ROW_ORDER NON_VOTING Threshold
NO NO YES 0.1
NO NO YES 0.3
NO NO YES 0.5
NO YES YES 0.75
YES YES YES 0.9

Extra Comparison with Iterative Closet Points:

I tried with Python, using sklearn package to run this method. Using a 2 sets of 30 points. Find one number of pair. Feed the same data with voting tree, it can’t find a full match and thus return.

The voting tree assumes a good matching with average similarity>=threshold because our pruning.

The non_voting method, on the other hand, returns the best matching possible, though it can be lower than the threshold.

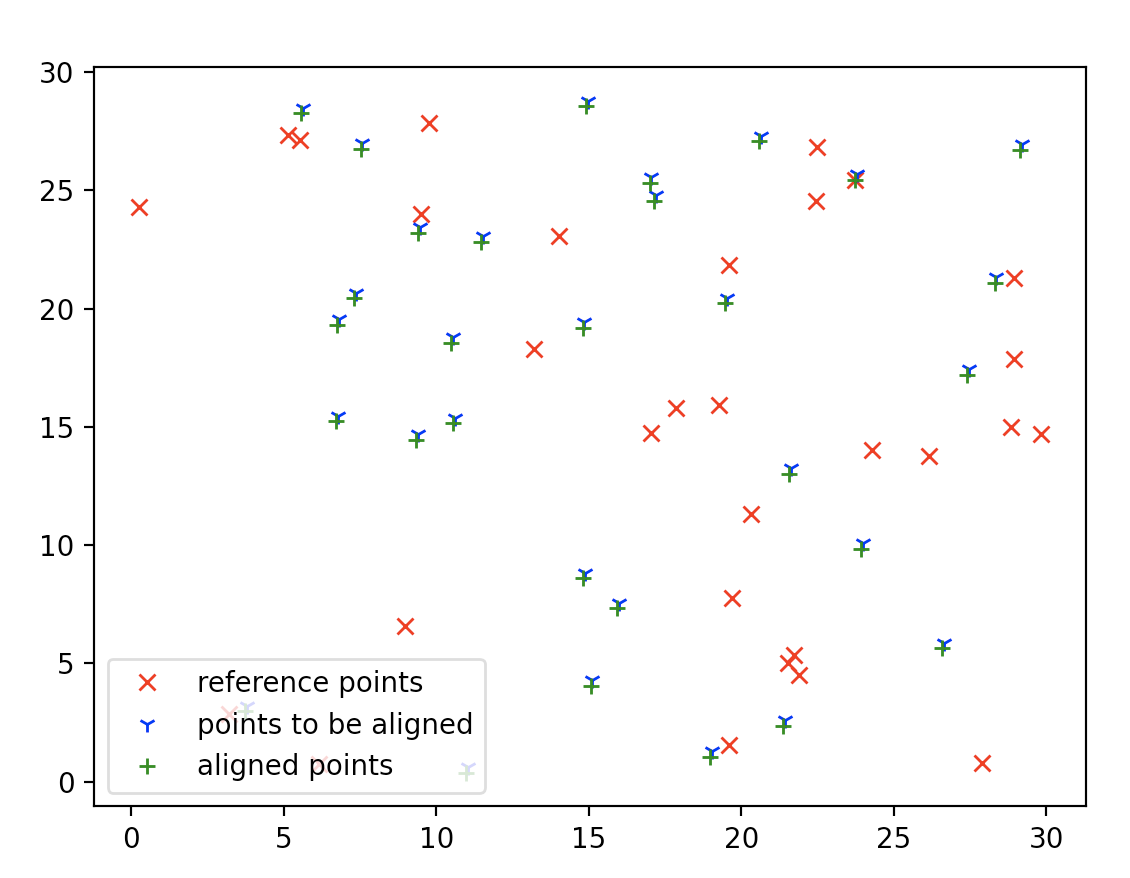
image-20211023014901237

On a small set of data (e.g. the sample case), the ICP solution can’t converge due to small amount of set size. However, if provided with a reasonable similar point set with a medium size (say, over 30). ICP method is reliable.

Besides, ICP has another strength is that, it can return partial matching, when there’s not a full match, it will return a partial match instead.

Chapter 4: Analysis and Comments

1.Build Tree:

Time Complexity:

  1. Build depth 1 children takes O(n) time, there are n nodes at depth 1.
  2. Using build helper to recursively build subtree takes $ O(n*T_{helper}(X))$

Since each node only takes O(1) to insert, the overall build tree time complexity equals to the number of nodes.

The number of nodes are:

$nA^m_m = nm!$

Overall Time Complexity (Without Pruning): $O(n*m!)$

Actually if we apply a rigorous threshold, and do pruning while building tree, we will only keep nodes at level 2 or shallower, and only one possible match down to the leaf. The time complexity can be reduced to $O(n^2)$ , since there are n*(n-m+1) nodes at depth 2 without pruning.

Space Complexity:

The Space Complexity = RecursionDepth*Recursion_assisted_space + size of tree.

  • Recursion Term: Recursion Depth = m (match at most m times)
  • $tree_size= nm!(node_size) = n*m!O(n-m) = O(n^2m!)$

Overall Space Complexity (Without Pruning): $O(n^2*m!)$

Samely if we apply a rigorous threshold, and do pruning while building tree, we will only keep nodes at level 2 or shallower, and only one possible match down to the leaf. The space complexity can be reduced to $O(n^3)$ , since there are $ n*(n-m+1)$ nodes at depth 2 without pruning. And each takes up to $O(n-m)$ space since it stores its children.

2.Futher Pruning:

Time Complexity (With rigorous pruning while build tree):

  1. In this step, we at most prune almost all nodes at depth 2 and some at depth 1, since if we use build-time pruning at step 1, most of nodes will not grow deeper than depth 2.
  2. For each node, we check its children (n-m at most) if its valid or not. And set isValid accordingly.
  • Number of check <=$ (depth 1 +depth 2)(n-m) = (n+n(n-m+1))*(n-m) = $O(n^3)$

Overall Time Complexity: $O(n^3)$

If not doing a rigorous pruning step while building, it takes nearly O(n*m!) to do the pruning

Space Complexity (With rigorous pruning while build tree):

  • This step doesn’t need extra space for memoization. However, it takes space for recursion. The space complexity equals to the max depth of the recursion, which is $O(m)$, since we the most depth is no deeper than 2 because of build-time pruning, except the best match path, takes $O(m)$ space for recursion.

If not doing a rigorous pruning step while building, it still takes O(m) to do the pruning, since the max depth is still $O(m)$

Overall Space Complexity: $O(m)$

3.Level Order Traversal

Time Complexity (With rigorous pruning):

  • Level Order traversal visit each node only once, which takes O(1) time, there are O(n^2) nodes if pruned rigorously.
  • If not pruned rigorously, in worst case, it could produce a result of O(n*m!)

Overall Time Complexity (Depend On Pruning): $(O(n^2),O(n*m!))$

Space Complexity (With rigorous pruning):

  • Level Order Traversal stores each node, each takes up to O(n) space.

Overall Space Complexity: $(O(n^2),O(n*m!))$

4.Compute Vote Count

Time Complexity:

  • This is similar to pruning step. We only compute those valid nodes, and check their children.

Overall Time Complexity (Depends On Pruning): $(O(n^3),O(n^2*m!))$

Space Complexity:

  • Space takes for recursion is the same as pruning step

Overall Space Complexity : $O(m)$

5.Voting

Time Complexity:

  • Once again, we traverse the tree, and each time we vote to either a map or 2D array.
  • There are up to $O(n*m!)$ nodes if not well pruned, but at least O(m) nodes.
  • If we uses a std::map for voting, this takes $O(log(n))$ time for insert, while 2D array only takes $O(1)$

Overall Time Complexity (Depends On Pruning): $(O(m),O(n*m!*log(n)))$

Space Complexity:

  • We keeps either a map or 2D array, the overall space is up to all possible pairs, which is n*m, but at least m, which means only one valid path after pruning.

Overall Time Complexity (Depend on table structure) : $(O(m),O(n*m))$

6.Decide Match (Voting)

Time Complexity:

  • SIMPLE_IDEA searches the largest m element in the table, if use sorting, this could takes, O(nlogn) times where n is the number of nodes.
  • ROW_ORDER searches the largest element in each line, which takes O(n*m) times, since there’re n rows and m columns.

Overall Time Complexity (Depends Table Structure): $(O(nlogn),O(n*m))$

Space Complexity:

  • This steps we use a vector to assist our 2D sorting. Which takes up to O(m) space.

Overall Time Complexity : $O(m)$

7.Decide Match (Non Voting)

Time Complexity:

  • We only visit leaf nodes and find out the node with maximum cumulative similarity.
  • And then we trace back to root from that node.
  • There are at most $(n*m!)$ leaf nodes at depth m, since we don’t prune in a non-voting method. Trace back only takes O(m) time.

Overall Time Complexity: $O(n*m!)$

Space Complexity:

  • This steps only takes constant space for storing the maximum cumulative similarity and its node..

Overall Time Complexity : $O(1)$

OVERALL

SIMPLE_IDEA (USE MAP AND VECTOR) ROW_ORDER(USE 2D VECTOR) NON_VOTING
Time Complexity: $O(n^2*m!)$ (Not pruning well) Time Complexity: $O(n^2*m!)$ (Not pruning well) Time Complexity: $O(n*m!)$
Time Complexity: $O(n^3)$ (Pruning well) Time Complexity: $O(n^3)$ (Pruning well) Time Complexity: $O(n*m!)$
Space Complexity:$O(n*m!)$ (Not Pruning Well) Space Complexity:$O(n*m!)$ (Not Pruning Well) Space Complexity:$O(n*m!)$
Space Complexity:$O(n^3)$ ( Pruning Well) Space Complexity:$O(n^3)$ ( Pruning Well) Space Complexity:$O(n*m!)$

It’s pretty obvious that, if we apply set up a good threshold, the ROW_ORDER and SIMPLE_IDEA both can have great time complexity performance. While the NON_VOTING method is an exponential method although it ensures correctness.

Extra: How to solve the problem of Mirrored Case

The reason we don’t get a good match when facing the mirrored case is that, we assume both polygons move in the same direction. And the solution is simple.

We add another n nodes at depth one, assume those point pairs moves in opposite direction, assume the first move clockwise and the second move counterclockwise. In this way, we can fix the problem.

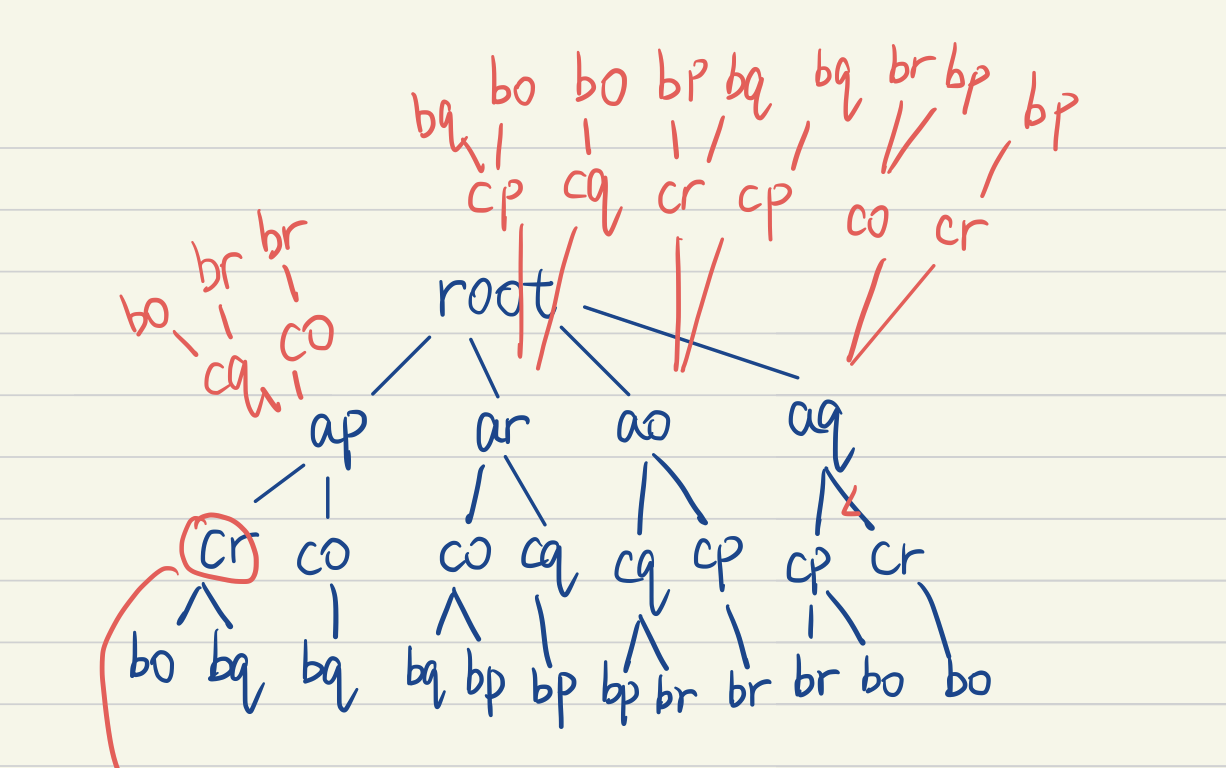
PNG图像 11

Nodes in red colors are indicating two polygons move in opposite direction, while the blue color ones move in the same direction. This address the mirror problem.

Appendix: Source Code (in C++11)

tree.hpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
#pragma once
#include <iterator>
#include <utility>
#include <tuple>
#include <iostream>
#include <unordered_map>
#include <string>
#include <memory>
#include <vector>
#include <unordered_set>
#include <sstream>
#include <set>
#include <stack>
#include <queue>
#include <map>
#include "geometry.hpp"
using std::map;
using std::vector;

/*
structure of the treenode
@memebers:
pointPair(contains the pair of points)
indices(contains the indices of points)
count(how many votes this node have)
isValid(if this node is a valid match, used for pruning)
depth(depth of the node)
credits(how many credits this node can spend, see report for details.
basically, a node with n credits can have n+1 child)
parent(the parent of the node)
children(the children of the node,indexing by the number of children)
*/
struct TreeNode
{
    //default constructor
    TreeNode()
    {
        pointPair.first = Point();
        pointPair.second = Point();
        count = 0;
        isValid = true;
        parent = nullptr;
    };

    //constructor
    TreeNode(Point &a, Point &b, TreeNode *parent, std::pair<int, int> indices, int depth, int credit)
    {
        this->pointPair = std::make_pair(a, b);
        this->indices = indices;
        this->depth = depth;
        this->credits = credit;
        this->parent = parent;
    };

    //corresponding points' coordinates
    std::pair<Point, Point> pointPair;
    //points' index respectively
    std::pair<int, int> indices;
    //how many votes it has, valid leaf node has 1 vote
    int count = 0;
    //check if the match is valid
    bool isValid = true;
    //the depth of current node
    int depth = 0;
    //how many credits it can use
    int credits = 0;
    //cumulative similarity along the path
    float cumulativeSim = 0.0f;
    //parent node
    TreeNode *parent;
    //we use points pairs' indices as key to get the TreeNode*
    //e.g. children[pair(1,2)] means get a children with pointsA[1] and pointsB[2]
    std::map<std::pair<int, int>, TreeNode *> children;
};

/*
the structure of the tree
@members:
root (root of the tree)
m,n (the size of point sets)
buildTree (build tree of point sets, with some pruning)
printTree (print all valid nodes in the tree, by level order)
invalidate (pruning step, see report for details)
levelOrder (get all valid nodes in the tree, by level order)
*/
class Tree
{

public:
    TreeNode *root;
    //size of pointsA and pointsB
    int m;
    int n;

    Tree(int m, int n)
    {
        root = new TreeNode();
        this->m = m;
        this->n = n;
    }

    ~Tree()
    {
        delete root;
    }

    //given a node and its indices, build its subtrees,but this time we don't pruning, used for non-voting method
    void buildHelperWithoutPruning(TreeNode *node, std::pair<int, int> indices, vector<Point> &pointsA, vector<Point> &pointsB)
    {
        //if it reaches the max depth, don't extend further
        if (node->depth == m)
            return;

        //if it has no credits, it can only have one child
        if (node->credits == 0)
        { // the children's index, only move one step
            auto idx = std::make_pair(indices.first + 1, (indices.second + 1) % n);
            // ready to calculate similarity
            vector<Point> a{node->parent->pointPair.first, node->pointPair.first, pointsA[idx.first]};
            vector<Point> b{node->parent->pointPair.second, node->pointPair.second, pointsB[idx.second]};
            // set new child, and assign similarity
            node->children[idx] = new TreeNode(pointsA[idx.first], pointsB[idx.second], node, idx, m, -1);
            node->children[idx]->cumulativeSim = node->cumulativeSim + Geo::similarity(a, b);
            return;
        }

        // if it still have credits, node can have credies+1 children
        else
        { //generate new children, node with k credits can have k+1 children
            for (int i = 1; i < node->credits + 2; i++)
            { // first index only move one step
                // second index can move 1~credits+1 steps
                auto idx = std::make_pair(indices.first + 1, (indices.second + i) % n);
                //generate new child
                node->children[idx] = new TreeNode(pointsA[idx.first], pointsB[idx.second], node, idx, node->depth + 1, node->credits - i + 1);
                //only nodes with depth>2 have valid parent and child
                if (node->depth >= 2)
                { //compute and assign similarity
                    vector<Point> a{node->parent->pointPair.first, node->pointPair.first, pointsA[idx.first]};
                    vector<Point> b{node->parent->pointPair.second, node->pointPair.second, pointsB[idx.second]};
                    node->children[idx]->cumulativeSim += node->cumulativeSim + Geo::similarity(a, b);
                }
            }
            //build subtrees for each child of current node
            for (auto &kv : node->children)
            {
                buildHelperWithoutPruning(kv.second, kv.first, pointsA, pointsB);
            }
        }

        return;
    };

    //given a node and its indices, build its subtrees
    //this is with build time pruning
    void buildHelper(TreeNode *node, std::pair<int, int> indices, vector<Point> &pointsA, vector<Point> &pointsB)
    {
        //if it reaches the max depth, don't extend further
        if (node->depth == m)
            return;

        //if it has no credits, it can only have one child
        if (node->credits == 0)
        {
            //check if the child is valid by comparing the triangle formed by point sets
            auto idx = std::make_pair(indices.first + 1, (indices.second + 1) % n);
            vector<Point> a{node->parent->pointPair.first, node->pointPair.first, pointsA[idx.first]};
            vector<Point> b{node->parent->pointPair.second, node->pointPair.second, pointsB[idx.second]};
            //if similarity is below the threshold, don't extend, set the node to invalid
            if (Geo::similarity(a, b) < Geo::threshold)
            {
                //if it has no children, this node itself is also not possible
                node->isValid = false;
                return;
            }

            //if similarity is above the threshold, extend it with the last node
            node->children[idx] = new TreeNode(pointsA[idx.first], pointsB[idx.second], node, idx, m, -1);
            return;
        }
        // if it still have credits, node can have credies+1 children
        else
        { //generate new children
            for (int i = 1; i < node->credits + 2; i++)
            { //second index can move 1~credits+1 steps
                auto idx = std::make_pair(indices.first + 1, (indices.second + i) % n);
                //pruning step, if the depth of node is same of greater than 2
                //check 2 triangles form by its parent and child and itself are similar
                if (node->depth >= 2)
                {
                    vector<Point> a{node->parent->pointPair.first, node->pointPair.first, pointsA[idx.first]};
                    vector<Point> b{node->parent->pointPair.second, node->pointPair.second, pointsB[idx.second]};
                    //if not similar, don't extend
                    if (Geo::similarity(a, b) < Geo::threshold)
                        continue;
                }
                //if it's shallower or is similar, extend
                node->children[idx] = new TreeNode(pointsA[idx.first], pointsB[idx.second], node, idx, node->depth + 1, node->credits - i + 1);
            }

            //check after the generate step, if the node have children
            //if it have no children, meaning the current match is invalid
            if (node->children.size() == 0)
            {
                node->isValid = false;
                return;
            }

            //build subtrees for each child of current node
            for (auto &kv : node->children)
            {
                buildHelper(kv.second, kv.first, pointsA, pointsB);
            }
        }

        return;
    };

    //buildTree from two lists of points, with build time pruning.
    TreeNode *buildTree(TreeNode *root, vector<Point> &pointsA, vector<Point> &pointsB)
    {
        //always keep pointsA having less or same points
        int m = pointsA.size();
        int n = pointsB.size();
        if (m > n)
        {
            std::swap(pointsA, pointsB);
            std::swap(m, n);
        }

        // the root node has n children, each children has n-m credits and depth 1
        for (int i = 0; i < n; i++)
        {
            auto idx = std::make_pair(0, i);
            root->children[idx] = new TreeNode(pointsA[idx.first], pointsB[idx.second], root, idx, 1, n - m);
        }

        //for the rest nodes, using helper function to build the subtree
        for (auto &kv : root->children)
        {
            buildHelper(kv.second, kv.first, pointsA, pointsB);
        }

        return root;
    };

    //buildTree from two lists of points, but no pruning this time;
    TreeNode *buildTreeWithoutPruning(TreeNode *root, vector<Point> &pointsA, vector<Point> &pointsB)
    {
        //always keep pointsA having less or same points
        int m = pointsA.size();
        int n = pointsB.size();
        if (m > n)
        {
            std::swap(pointsA, pointsB);
            std::swap(m, n);
        }

        // the root node has n children, each children has n-m credits and depth 1
        for (int i = 0; i < n; i++)
        {
            auto idx = std::make_pair(0, i);
            root->children[idx] = new TreeNode(pointsA[idx.first], pointsB[idx.second], root, idx, 1, n - m);
        }

        //for the rest nodes, using helper(without pruning) function to build the subtree
        for (auto &kv : root->children)
        {
            buildHelperWithoutPruning(kv.second, kv.first, pointsA, pointsB);
        }

        return root;
    };

    //invalidate the node if it has no children, or all of its children are invalid
    //top-down
    //FURTHER PRUNING IN THE REPORT
    void invalidate(TreeNode *node)
    {
        //if the node has no children and it's not a leaf
        //meaning that the node is invalid
        if (node->children.size() == 0 && node->depth < m)
        {
            node->isValid = false;
            return;
        }

        //if it has children
        if (node->children.size() != 0)
        {
            node->isValid = false;
            //if some of its children are valid, the node should be valid
            for (auto &kv : node->children)
            {
                node->isValid = node->isValid || kv.second->isValid;
            }
        }

        //this means the node has no valid children
        if (!node->isValid)
        {
            return;
        }

        //invalidate the children of the node
        for (auto &kv : node->children)
        {
            invalidate(kv.second);
        }
    };

    //print tree node indices by level order, but only print those valid
    void printTree()
    {
        auto nodes = levelOrder(root);
        //skip the dummy root
        for (int i = 1; i < nodes.size(); i++)
        {
            for (int j = 0; j < nodes[i].size(); j++)
            {
                std::cout << '(' << 1 + nodes[i][j]->indices.first << ',' << 1 + nodes[i][j]->indices.second << ')';
            }
            std::cout << std::endl;
        }
    };

    //get the nodes of trees by level order
    vector<vector<TreeNode *>> levelOrder(TreeNode *root)
    {
        if (root == nullptr)
            return {};

        vector<vector<TreeNode *>> ans;
        vector<TreeNode *> cur, next;
        //the nodes to process in current/next step;

        cur.push_back(root);

        while (!cur.empty())
        {
            for (auto node : cur)
            {
                for (auto &kv : node->children)
                    //only process valid nodes
                    if (kv.second->isValid)
                        next.push_back(kv.second);
            }
            ans.push_back(cur);

            swap(cur, next);
            next.clear();
        }

        return ans;
    };
};

geometry.hpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#pragma once
#include "tree.hpp"

/*
store the coordinate of a 2D point
With some computing method
*/
struct Point
{
    float x;
    float y;

    Point()
    {
        this->x = 0.0f;
        this->y = 0.0f;
    }

    // constructor
    Point(float x, float y)
    {
        this->x = x;
        this->y = y;
    }
    // format the point
    void print() const
    {
        std::cout << '(' << this->x << ',' << this->y << ')';
    };
};

//Some utility functions of Geometric computation
namespace Geo
{
    using namespace std;
    const float pi = 3.1415926;

    // threshold of similarity between two polygons
    // a good threshold is 0.7~0.9 in simple case
    const float threshold = 0.9f;

    /*
    convert radians to degrees
    */
    float toDegree(float rad)
    {
        return rad * 180.f / pi;
    };

    //get length of the edge between two points;
    float getLength(Point &a, Point &b)
    {
        float dx = abs(a.x - b.x);
        float dy = abs(a.y - b.y);
        return sqrtf(dx * dx + dy * dy);
    };

    /*
    @description: a is in the middle of b and c
    this functions returns the angle CAB or simply angle A
    @assumption: assume convex polygon, only return non-reflex angle
    */
    float getAngle(Point &a, Point &b, Point &c)
    {
        float AB = getLength(a, b);
        float BC = getLength(b, c);
        float AC = getLength(a, c);

        float cosA = (AB * AB + AC * AC - BC * BC) / (2 * AB * AC);
        return toDegree(acos(cosA));
    };

    /*
    compute similarity between two sets of points(2 polygons)
    the sets should have the same size.
    For details, see report.
    */
    float similarity(vector<Point> &a, vector<Point> &b)
    {

        float res;
        int n = a.size();

        /*
        don't take similarity between lines into account
        */

        if (n < 3)
            return 1.0;

        //similarity between edges
        float simLenUpper = 0;
        float simLenLower = 0;

        for (int i = 0; i < n - 1; i++)
        {
            float edgeA = getLength(a[i], a[i + 1]);
            float edgeB = getLength(b[i], b[i + 1]);
            simLenLower += abs(edgeA + edgeB);
            simLenUpper += abs(edgeA - edgeB);
        }

        //the last edge between the first and the last point
        float edgeA = getLength(a[0], a[n - 1]);
        float edgeB = getLength(b[0], b[n - 1]);
        simLenLower += abs(edgeA + edgeB);
        simLenUpper += abs(edgeA - edgeB);

        //edge coefficient 0.5 by default
        res += 0.5 * (1 - simLenUpper / simLenLower);

        //similarity between angles
        float simAngUpper = 0;
        for (int i = 1; i < n - 1; i++)
        {
            float angA = getAngle(a[i], a[i + 1], a[i - 1]);
            float angB = getAngle(b[i], b[i + 1], b[i - 1]);
            simAngUpper += abs(angA - angB);
        }

        //last 2 angles
        float angA = getAngle(a[0], a[n - 1], a[1]);
        float angB = getAngle(b[0], b[n - 1], b[1]);
        simAngUpper += abs(angA - angB);
        angA = getAngle(a[n - 1], a[n - 2], a[0]);
        angB = getAngle(b[n - 1], b[n - 2], b[0]);
        simAngUpper += abs(angA - angB);

        //angle coefficient 0.5 by default
        res += 0.5 * (1 - simAngUpper / 180.f);

        return res;
    };
}

main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
#include "tree.hpp"
#include "geometry.hpp"
/*
USAGE ON MACROS:
_ROW_ORDER: VOTING TABLE ROW_ORDERED METHOD
_NON_VOTING: NON VOTING METHOD
_VOTE_ORDER: SIMPLE IDEA METHOD
_USER_INPUT: GET INPUT FROM USER

AVAIABLE CASES:
    _SAMPLE_CASE1~4
    MIRROR
*/

// #define _ROW_ORDER
#define _SAMPLE_CASE1
// #define _NON_VOTING
#define _VOTE_ORDER

/*
TO USE: set C++ standard to C++11 or later
Read "README.md" first.
*/

/*
@params:levelOrder,votingTable,maxDepth
@return:isFullMatch
@description:1.compute how many votes each nodes has 2. visit each valid node, and vote
*/
bool voting(vector<vector<TreeNode *>> &levelOrder, map<std::pair<int, int>, int> &table, int maxDepth)
{
    //this means no path can be length m, meaning no full match
    if (levelOrder.size() < maxDepth)
    {
        std::cout << "No Full Match Under Such Similarity Setting" << std::endl;
        return false;
    }
    // check the degree of each node, and only visit each node once
    // leaf as one count
    // node.count = node->left.count+node->right.count;
    // compute from bottom up

    //compute each node has how many votes,skip the dummy root
    for (int i = levelOrder.size() - 1; i >= 0; i--)
    {
        for (int j = 0; j < levelOrder[i].size(); j++)
        {
            //leaf nodes has one vote
            if (levelOrder[i][j]->depth == maxDepth)
            {
                levelOrder[i][j]->count = 1;
                continue;
            }
            //non-leaf nodes have vote equals to its all valid children
            for (auto &kv : levelOrder[i][j]->children)
                levelOrder[i][j]->count += kv.second->count;
        }
    }

    //after computing how many votes each node has, we need to calculate the final vote count
    //voting process
    for (int i = 1; i < levelOrder.size(); i++)
    {
        for (int j = 0; j < levelOrder[i].size(); j++)
        {
            table[levelOrder[i][j]->indices] += levelOrder[i][j]->count;
        }
    }

    return true;
};

int main()
{
    using namespace std;

    //two vectors to store input
    vector<Point> pointsA;
    vector<Point> pointsB;

    //size of pointsA and pointsB
    int m, n;

//compute answer from user input
#ifdef _USER_INPUT
    scanf("%d %d", &m, &n);
    for (int i = 0; i < m; i++)
    {
        float x, y;
        scanf("%f %f", &x, &y);
        pointsA.push_back(Point(x, y));
    }

    for (int i = 0; i < n; i++)
    {
        float x, y;
        scanf("%f %f", &x, &y);
        pointsB.push_back(Point(x, y));
    }
#endif

#ifdef _SAMPLE_CASE1
    // Sample Case
    pointsA.clear();
    pointsB.clear();
    pointsA.push_back(Point(0, 4));
    pointsA.push_back(Point(3, 0));
    pointsA.push_back(Point(0, 0));
    pointsB.push_back(Point(8, 4));
    pointsB.push_back(Point(8, 1));
    pointsB.push_back(Point(4.25, 6));
    pointsB.push_back(Point(8, 6));
#endif

// a small square and a 2x square
#ifdef _SAMPLE_CASE2
    // Sample Case
    pointsA.clear();
    pointsB.clear();

    pointsA.push_back(Point(0, 0));
    pointsA.push_back(Point(0, 1));
    pointsA.push_back(Point(1, 1));
    pointsA.push_back(Point(1, 0));

    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 1));
    pointsB.push_back(Point(0, 2));
    pointsB.push_back(Point(1, 2));
    pointsB.push_back(Point(2, 2));
    pointsB.push_back(Point(2, 1));
    pointsB.push_back(Point(2, 0));
    pointsB.push_back(Point(1, 0));

#endif

// a small triangle and a pentagon
#ifdef _SAMPLE_CASE3
    // Sample Case
    pointsA.clear();
    pointsB.clear();

    pointsA.push_back(Point(0, 0));
    pointsA.push_back(Point(0, 1));
    pointsA.push_back(Point(1, 1));

    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 1));
    pointsB.push_back(Point(1, 1));
    pointsB.push_back(Point(2, 1));
    pointsB.push_back(Point(2, 4));

#endif

// a large case to test speed performance (M=21,N=28)
#ifdef _SAMPLE_CASE4
    // Sample Case
    pointsA.clear();
    pointsB.clear();
    pointsA.push_back(Point(0, 4));
    pointsA.push_back(Point(3, 0));
    pointsA.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(-3, 0));
    pointsB.push_back(Point(0, 4));
    pointsB.push_back(Point(8, 6));
    pointsA.push_back(Point(0, 4));
    pointsA.push_back(Point(3, 0));
    pointsA.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(-3, 0));
    pointsB.push_back(Point(0, 4));
    pointsB.push_back(Point(8, 6));
    pointsA.push_back(Point(0, 4));
    pointsA.push_back(Point(3, 0));
    pointsA.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(-3, 0));
    pointsB.push_back(Point(0, 4));
    pointsB.push_back(Point(8, 6));
    pointsA.push_back(Point(0, 4));
    pointsA.push_back(Point(3, 0));
    pointsA.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(-3, 0));
    pointsB.push_back(Point(0, 4));
    pointsB.push_back(Point(8, 6));
    pointsA.push_back(Point(0, 4));
    pointsA.push_back(Point(3, 0));
    pointsA.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(-3, 0));
    pointsB.push_back(Point(0, 4));
    pointsB.push_back(Point(8, 6));
    pointsA.push_back(Point(0, 4));
    pointsA.push_back(Point(3, 0));
    pointsA.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(-3, 0));
    pointsB.push_back(Point(0, 4));
    pointsB.push_back(Point(8, 6));
    pointsA.push_back(Point(0, 4));
    pointsA.push_back(Point(3, 0));
    pointsA.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(-3, 0));
#endif

//this actually got problems, but if we got a match, the overall polygon matching is actually correct,
//we only have to reorder the indices order
#ifdef MIRROR
    // MIRROR Case
    pointsA.clear();
    pointsB.clear();
    pointsA.push_back(Point(0, 4));
    pointsA.push_back(Point(3, 0));
    pointsA.push_back(Point(0, 0));
    pointsB.push_back(Point(0, 0));
    pointsB.push_back(Point(-3, 0));
    pointsB.push_back(Point(0, 4));
    pointsB.push_back(Point(8, 6));
#endif

    // ensureing pointsA always have smaller size
    if (pointsA.size() > pointsB.size())
        swap(pointsA, pointsB);

    /*
    using map for voting table, where key is the point pair indicies
    here we have to use map instead of unordered_map
    because type(pair<int,int>) in C++ STL is not hashable
    */
    map<pair<int, int>, int> votingTable;

    /*
    Initialize Tree with given points array
    */
    Tree tree(pointsA.size(), pointsB.size());

/*
in non voting method, we didn't prune the tree
we calculate the the cumulative Similarity of all the leaf nodes
finding out the one with cumulative largest similarity
*/
#ifdef _NON_VOTING
    std::chrono::time_point<std::chrono::system_clock> start, end;
    start = std::chrono::system_clock::now();

    //build tree without pruning
    auto root = tree.buildTreeWithoutPruning(tree.root, pointsA, pointsB);

    //get valid tree nodes by level order traversal
    auto nodes = tree.levelOrder(root);
    //leaf nodes are at the last level
    auto leaves = nodes[nodes.size() - 1];

    //compare and find out the node with largest cumulative similarity
    float maxSum = 0.f;
    TreeNode *maxNode = nullptr;
    for (auto leaf : leaves)
    {
        if (leaf->cumulativeSim > maxSum)
        {
            maxSum = leaf->cumulativeSim;
            maxNode = leaf;
        }
    }

    //after finding the max cumulativeSimilarity
    //trace back bottom up, push the path to result
    vector<pair<int, int>> res;
    while (maxNode->parent != nullptr)
    {
        res.push_back(maxNode->indices);
        maxNode = maxNode->parent;
    }

    //print out the path
    for (int i = res.size() - 1; i >= 0; i--)
    {
        cout << '(' << 1 + res[i].first << ", " << 1 + res[i].second << ')' << endl;
    }
    std::chrono::duration<double> duration;
    end = std::chrono::system_clock::now();
    duration = end - start;
    //print time it takes
    std::cout << duration.count() << " seconds" << std::endl;
#endif

// this contains build/prune/level order/vote 4 steps
#ifndef _NON_VOTING
    std::chrono::time_point<std::chrono::system_clock> start, end;
    start = std::chrono::system_clock::now();

    //build tree with build time pruning
    auto root = tree.buildTree(tree.root, pointsA, pointsB);

    // further pruning step
    tree.invalidate(root);

    // print the valid nodes in the tree, for test
    // tree.printTree();

    // //get valid tree nodes by level order traversal
    auto nodes = tree.levelOrder(root);

    //check if there's a full match, also doing the voting
    bool isFullMatch = voting(nodes, votingTable, pointsA.size());

    //if no full match, return with -1
    if (!isFullMatch)
        return -1;

#endif

// a method ensuring no collision match, with possibility of wrong-matching but no collision
#ifdef _ROW_ORDER
    int loop_count = 1;
    //verbose means if print the result or not
    std::function<void(bool)> row_order = [&](bool verbose)
    {
        // we use a 2D matrix to represent the table
        vector<vector<int>>
            res(pointsA.size(), vector<int>(pointsB.size(), 0));

        // convert the std::map into 2D vector
        for (auto &kv : votingTable)
        {
            res[kv.first.first][kv.first.second] = kv.second;
        }

        //traverse each row, find out the max element
        for (int i = 0; i < res.size(); i++)
        {
            for (int j = 0; i < res[i].size(); j++)
            {
                //if the element has the most votes in the row
                if (res[i][j] == *max_element(res[i].begin(), res[i].end()))
                {
                    if (verbose)
                        //print out the indicies
                        cout << '(' << 1 + i << ", " << 1 + j << ')';

                    //disable the column, in case next row matches the same column
                    for (int i = 0; i < res.size(); i++)
                    {
                        res[i][j] = 0;
                    }

                    break;
                }
            }
            if (verbose)
                cout << endl;
        }
    };

    std::chrono::duration<double> duration;

    // loop for k times
    for (int i = 0; i < loop_count; i++)
    {
        row_order(true);
    }

    //calculate the time performance
    end = std::chrono::system_clock::now();
    duration = end - start;
    std::cout << duration.count() << " seconds" << std::endl;
#endif

//this is the SIMPLE_IDEA in the report
//print m matches with top most votes, collision could happen with a low threshold
#ifdef _VOTE_ORDER
    int loop_count = 1;
    //verbose means if print the result or not
    std::function<void(bool)> order = [&](bool verbose)
    {
        //getting matches with order of votes, using with restrict threshold of similarity
        vector<pair<pair<int, int>, int>>
            pairs;

        //convert map to vector
        for (auto itr = votingTable.begin(); itr != votingTable.end(); ++itr)
            pairs.push_back(*itr);

        //sort voting table by its vote count
        sort(pairs.begin(), pairs.end(), [](pair<pair<int, int>, int> &a, pair<pair<int, int>, int> &b)
             { return a.second < b.second; });

        // print the first m highest votes
        for (int i = 0; i < pointsA.size(); ++i)
        {
            if (verbose)
                cout << '(' << 1 + pairs[i].first.first << ", " << 1 + pairs[i].first.second << ')' << endl;
        }
    };

    std::chrono::duration<double> duration;
    start = std::chrono::system_clock::now();

    //loop for loop_count times
    for (int i = 0; i < loop_count; i++)
    {
        order(true);
    }

    end = std::chrono::system_clock::now();
    duration = end - start;
    std::cout << duration.count() << " seconds" << std::endl;
#endif

    // SOME TEST CODES TO TEST UTILITY FUNCTIONS
    // auto pp = root->children[make_pair(0, 0)]->children[make_pair(1, 1)]->pointPair;

    // pp.first.print();
    // pp.second.print();
    // cout << Geo::similarity(pointsA, pointsB) << endl;
    // cout << Geo::getAngle(pointsA[0], pointsA[1], pointsA[2]) << endl;

    // SOME TEST CODES TO TEST INPUT
    // for (const auto &point : pointsA)
    // {
    //     point.print();
    // }
}