1463. Cherry Pickup II

Description:

You are given a rows x cols matrix grid representing a field of cherries where grid[i][j] represents the number of cherries that you can collect from the (i, j) cell.

You have two robots that can collect cherries for you:

• Robot #1 is located at the top-left corner (0, 0), and
• Robot #2 is located at the top-right corner (0, cols - 1).

Return the maximum number of cherries collection using both robots by following the rules below:

• From a cell (i, j), robots can move to cell (i + 1, j - 1), (i + 1, j), or (i + 1, j + 1).
• When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
• When both robots stay in the same cell, only one takes the cherries.
• Both robots cannot move outside of the grid at any moment.
• Both robots should reach the bottom row in grid.

Example 1:

1
2
3
4
5
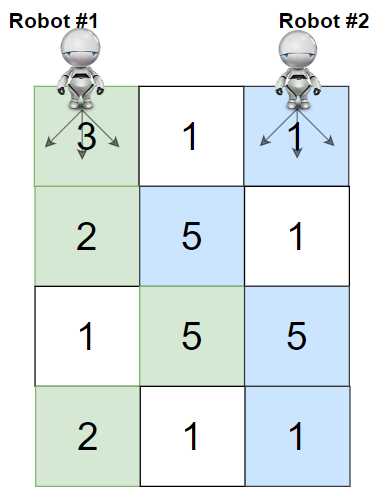
6

Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
Output: 24
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.

Example 2:

1
2
3
4
5
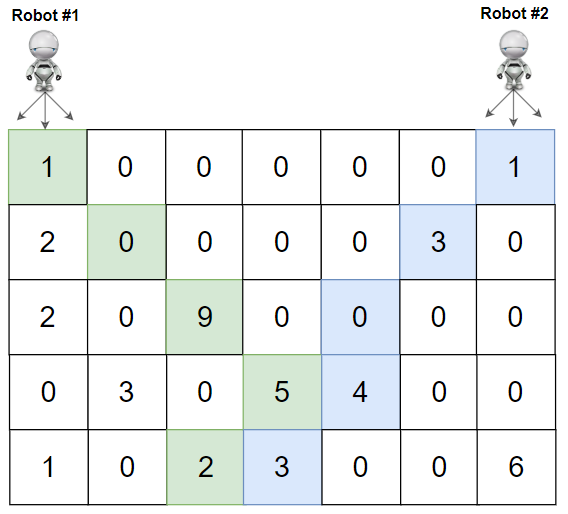
6

Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
Output: 28
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.

Constraints:

• rows == grid.length
• cols == grid[i].length
• 2 <= rows, cols <= 70
• 0 <= grid[i][j] <= 100

We have a maximum input size of 70*70 = 4900, a loose limit would be $O((mn)^2)$.

Intuition:

• Each round, each robot would go exactly one step down. And they will always move forward until reaching the end.
  • In this way, we can describe the status of two robots by a 3-element tuple (y,x1,x2). Since #y: row #x: col, there are $O(r*c^2)$ combinations
• dp[y][x1][x2] means the maximum cherries collected at this combination
• Base Case: y>=r, x<0 or x>c (out of bounary), return 0
• Transition Equation: dp[y+1][x1][x2] ={max[y][x1'][x2'] + grid[y][x1]+grid[y][x2] if x1!=x2 else 0}
• Time Complexity: $O(rc^29)$
• Space Complexity: $O(r*c^2)$
• To get the answer: find the maximum value in dp[r-1][x1][x2] (traverse)

A Reverse Solution:

Robots start at any grid in the last level, and then they go up until one goes to the left corner, the other go to the right corner.

• Transition Equation: dp[y][x1][x2] ={max[y+1][x1'][x2'] + grid[y][x1]+grid[y][x2] if x1!=x2 else 0}

• To get the answer: dp[0][0][c-1]

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

class Solution
{
    using triArr = vector<vector<vector<int>>>;
    int r = 0;
    int c = 0;

public:
    int cherryPickup(vector<vector<int>> &grid)
    {
        this->r = grid.size();
        this->c = grid[0].size();
        triArr dp(r, vector<vector<int>>(c, vector<int>(c, -1)));
        return helper(0, 0, c - 1, grid, dp);
    }

    // used for recursion
    int helper(int y, int x1, int x2, vector<vector<int>> &grid, triArr &dp)
    {
        if (x1 < 0 || x1 >= c || x2 < 0 || x2 >= c || y >= r || y < 0)
        {
            return 0;
        }

        int ans = dp[y][x1][x2];
		
        //if visited return
        if (ans != -1)
            return ans;

        bool isSame = x1 == x2;
        int cur = grid[y][x1] + (isSame ? 0 : grid[y][x2]);
        for (int d1 = -1; d1 <= 1; d1++)
        {
            for (int d2 = -1; d2 <= 1; d2++)
            { // each round find the max one from 9 combinations
                ans = max(ans, cur + helper(y + 1, x1 + d1, x2 + d2, grid, dp));
            }
        }
		
        //update the answer
        dp[y][x1][x2] = ans;
        return ans;
    }
};