382. Linked List Random Node

Description:

Given a singly linked list, return a random node’s value from the linked list. Each node must have the same probability of being chosen.

Implement the Solution class:

• Solution(ListNode head) Initializes the object with the integer array nums.
• int getRandom() Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be choosen.

Example:

1
2
3
4
5

Input
["Solution", "getRandom", "getRandom", "getRandom", "getRandom", "getRandom"]
[[[1, 2, 3]], [], [], [], [], []]
Output
[null, 1, 3, 2, 2, 3]

Constraints:

• The number of nodes in the linked list will be in the range [1, 104].
• -10^4 <= Node.val <= 10^4
• At most 10^4 calls will be made to getRandom.

Since at most 10k calls will be made, the overall time complexity of each random call is expected to be bounded by O(nlogn).

Intuition:

A simple approach would be converting the linked list into an array, and then random generate a number and random access the array. This would cost extra O(n) space for keeping an array, and O(1) to random access the array.

Actually, another implementation is that, we could traverse the list to get the length, and then random generate a number, and then take O(n) step to get the number.

This implementation would take O(1) extra space, and O(n) for traversing and accessing.

What if… just visit each node only once and use O(1) space?

The key is, Each node must have the same probability of being chosen.

So to ensure the same probability, it is not necessary to use the built-in random function.

Introducing Reservoir Sampling:

I found a video on YouTube, explaining this idea in an interesting and great way.

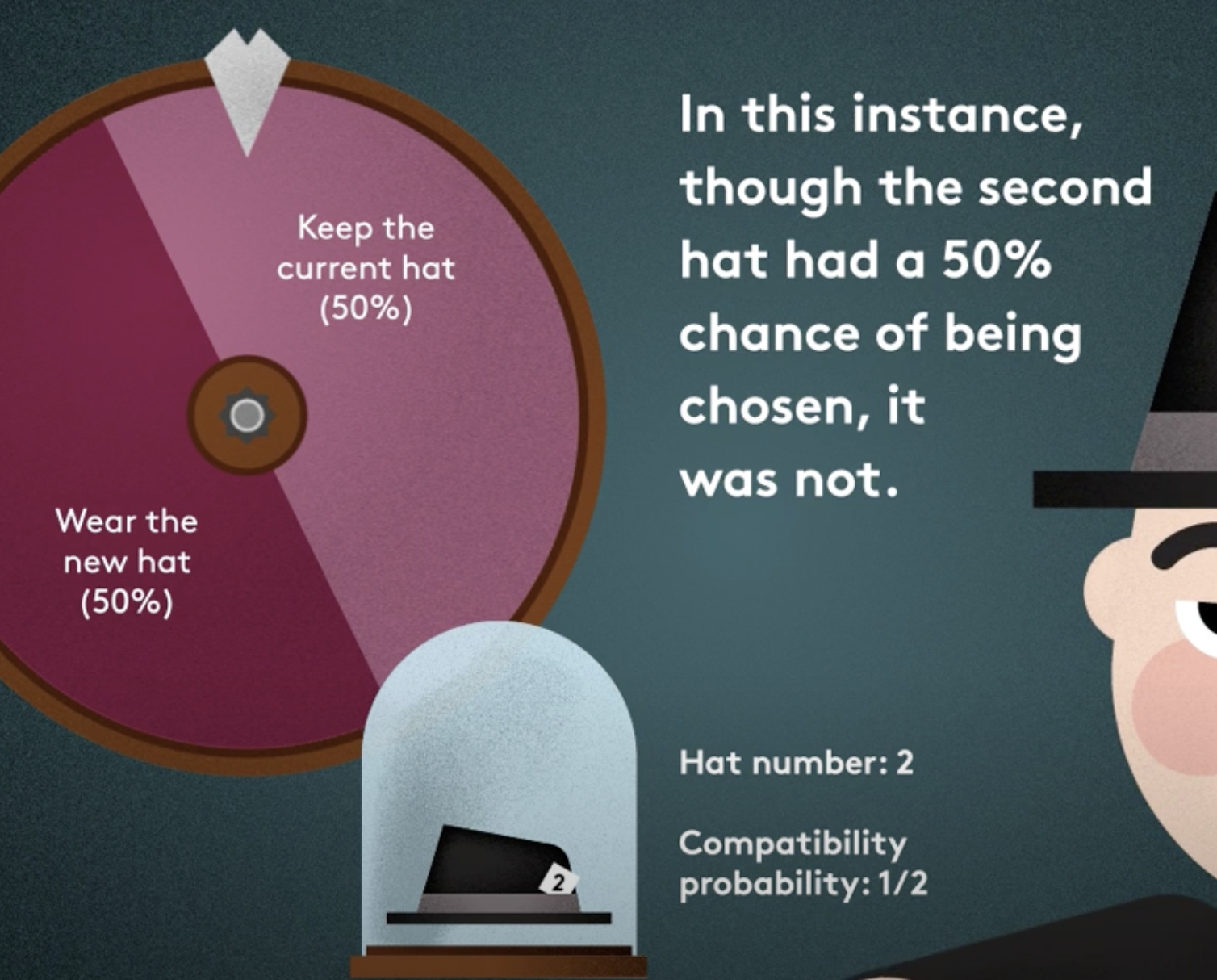
• Scenario: A man picking a hat

  • each round replace the old hat or wear new hat

  • Each round probability of wearing new hat: 1/n

  • The first hat has a chance of 1/1, so he 100% wear the hat

  • The second hat has a chance of 1/2, so he 50% wear the 2nd hat, 50% keep the first hat

  • The third hat has a chance of 1/3, 1/3 wear the 3nd hat, 2/3 keep the original hat

  • So on and so forth…

The Good Side:

Reservoir sampling doesn’t need to know the length of the list in advance, it’s an online random algorithm.

Proof on Equal Probability:

The $i_{th}$ hat has a probability of $\frac{1}{i}$ of being chosen in its round. The probability of $i_{th}$ hat being chosen after $n$ times can be given as:

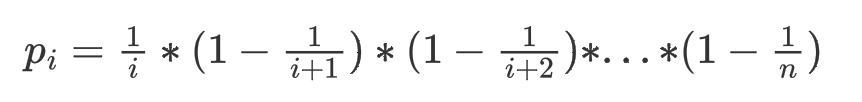
Which is the multiplication of $i_{th}$ hat being chosen, and all the hats after $i_{th}$ hat not being chosen.

And this RHS equals to $\frac{1}n$, which means every hat has the same probability of being chosen.

• Link: https://www.youtube.com/watch?v=A1iwzSew5QY

Implementation:

Now let’s implement the Reservoir Sampling into our code, note that we still have to simulate the process of spinning the wheel, using the random function to implement. And it’s generally slower to perform floating point division, use integer instead.

• Instead of 1/i, we have 1,2,3…i, but only the 1 means being chosen
• i start from 1, because it’s not valid to divide by 0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

#include "header.hpp"

// reservoir sampling
class Solution
{
private:
    const ListNode *head;

public:
    Solution(ListNode *head)
    {
        this->head = head;
    }

    int getRandom() const
    {
        // we are not allowed to modify the head pointer itself
        // each round we create a new node to do the trick
        auto node = head;
        int res = head->val;
        int i = 1;
        while (node != nullptr)
        {

            // random generate 1~i, only 1 means being selected
            // i should start from 1, or there would be divide by 0 issue
            bool replace = (rand() % (i - 1 + 1)) + 1 == 1;
            if (replace)
                res = node->val;
            node = node->next;
            i++;
        }

        return res;
    }
};

/**
 * Your Solution object will be instantiated and called as such:
 * Solution* obj = new Solution(head);
 * int param_1 = obj->getRandom();
 */