98.Validate Binary Search Tree

Description:

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

Examples:

1
2
3
4
5
6

Input: root = [2,1,3]
Output: true

Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -2^31 <= Node.val <= 2^31 - 1

Note:

Property of a Binary Search Tree:

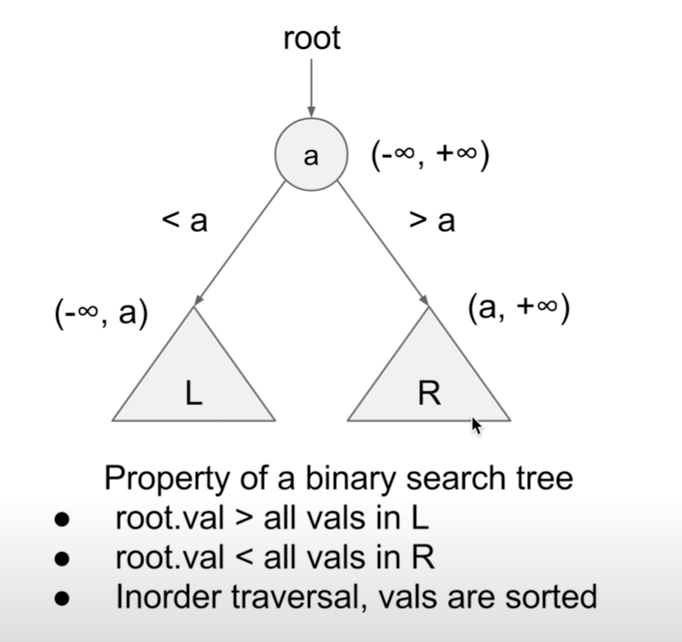
Ref from Huahua@Youtube

For each TreeNode

• cur->left->val < cur->val
• cur->right->val > cur->val

Consider the range:

The input value ranges from -2^31 <= Node.val <= 2^31 - 1, so the positive/negative infinity should be set to LLONG_MIN, LLONG_MAX. (64-bit)

Pseudocode:

1
2
3
4
5
6
7
8
9

if nulltree:
	return true;

//if the node val is beyond the range, it's invalid.
if node->val<=min_val||node->val>=max_val:
	return false;

//check subtree of both sides
return validate(cur->left,min,cur->val)&&validate(cur->right,cur->val,max)

C++:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution
{
public:
    bool isValidBST(TreeNode *root)
    {
        return isValidBST(root, LONG_MIN, LONG_MAX);
    }
    bool isValidBST(TreeNode *root, long mn, long mx)
    {
        if (!root)
            return true;
        if (root->val <= mn || root->val >= mx)
            return false;
        return isValidBST(root->left, mn, root->val) && isValidBST(root->right, root->val, mx);
    }
};

For Your Consider:

What if the range extends to -2^64 ~2^64-1?

Hint: Use nullptr to represent infinity.